Young’s equation expresses the equilibrium situation:
gSV - gLS = gLV cos q

where q is the contact angle. The left hand side is what we can calculate from the things we can measure on the right hand side. We can only calculate the difference between the two quantities on the left hand side. In essence, gSV hides behind gLS, which is the interfacial tension between the liquid and solid. We have one equation and two unknowns.

There is no exact answer to this dilemma. There are models which provide approximate answers by giving us another equation with which to separate gSV and gLS. It is very important to under-stand that these are, indeed, very approximate. The models are based on independent knowledge of how liquids and solids adhere to one another. There are seven models, which are widely used, and a number of others which have their own small followings. These seven models are often called by different names, so it becomes tedious to keep track of all of them. For the record, these models and their synonyms are

     Zisman critical wetting tension
     Fowkes
     Owens, Wendt geometric mean
     Extended Fowkes
     Wu harmonic mean
     Lewis acid/base theory
     Equation-of-state

For well-known, well-characterized surfaces, there can be a 25% difference in the answers provided by each model. Each model does better with one type of surface or another, but there is no recognized “correct” answer.

Why do people bother with surface energy? Primarily they would like to characterize surfaces without having to explicitly describe the test fluid. The right hand side of Young’s equation is the product of the test liquid surface tension and the contact angle, so surface energy is more “fundamental,” even if it cannot be accurately measured with today’s understanding.? Secondly, the surface energy description mimics the surface tension description for liquids, so similar terminology is used for both. Thirdly, the inaccuracies in today’s models are acceptable to some.

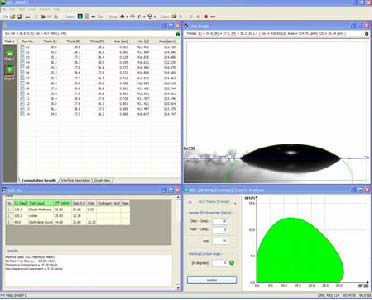
Calculation procedures of surface energy on MD software:

     Measure contact angles with test fluids for which you know the surface tension.

     Click on the icon SE in the toolbar, choose a method to supply the missing equation. See what others in your industry have chosen.

     Enter the surface tension for the test liquids and the measured contact angles for each in the Surface Energy Computation. This is purposefully left as a manual transfer because you may wish to average many readings before entering the data. After you choose the model, you click re-computationand the equations are solved.

In one sense, this is very easy, taking only three steps. However, in another sense, it is subtle because you are restricting the available answers when you choose the model. The real issue is choosing a model.

A good place to start is the Equation-of-state method with water as the test liquid. This is the simplest and gives a good idea of what the surface energy is. The Fowkes method is best at low contact angles and worst at high. Because the method has an adjustable parameter, F, which is normally set equal to 1, the model can be tweaked to provide better answers at high contact angles. By “better,” we mean more like the other methods. To do this, we must have a “known” surface energy and contact angle. We use Teflon as the reference material and call this the extended Fowkes method.

Finally, most workers use surface energy numbers on a relative basis in the final analysis. For example, if they wish to increase the wettability of a polymer by plasma treatment, they would be happy by a change of 25 to 35 but they would be just as happy with a change of 30 to 40.